Jamovi | Introducción a la prueba Chi-cuadrado de independencia

En la entrada anterior hemos visto que el análisis de bondad de ajuste Chi-cuadrado sirve para analizar y comparar la frecuencia observada con la frecuencia esperada de una variable cualitativa nominal. ¿Qué pasa cuando queremos analizar la relación entre dos variables cualitativas? Pues que tenemos que realizar la prueba Chi-cuadrado de independencia (Chi-square test of Independence en inglés), también conocido como Chi-cuadrado de Pearson o Chi-cuadrado de asociación.

Prueba Chi-cuadrado de independencia

Al igual que ocurre con la prueba T de Student o el ANOVA de un factor, la prueba chi-cuadrado de independencia es un contraste de hipótesis que se usa para comparar diferencias significativas en las frecuencias de dos variables categóricas. 

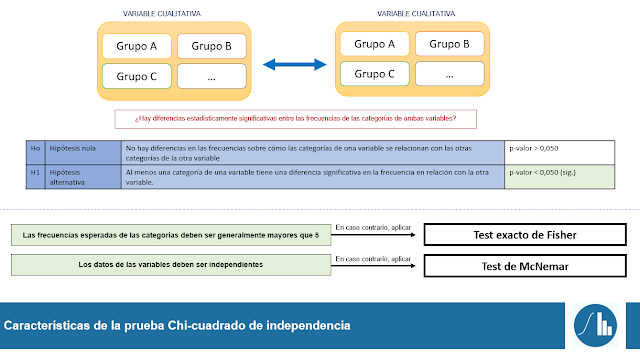
Puesto que tenemos dos variables cualitativas categóricas (ya sean nominales u ordinales) con distintas categorías o tipos, se suele declarar el número de categorías que tiene cada una de las variables objeto de estudio. Es decir, es muy habitual expresar este análisis como una prueba Chi-cuadrado z · y (en donde z es el número de categorías de la variable A e y es el número de categorías de la variable B). En la siguiente ilustración se muestran las hipótesis estadística de partida de dicha prueba, que se deberán adaptar a las características particulares de cada experimento:

Tal y como se aprecia en la imagen anterior, para realizar el test Chi-cuadrado de independencia ambas variables cualitativas categóricas deben tener una frecuencia esperada grande (normalmente mayor de 5) y los datos deben ser independendientes (de ahí el nombre de la prueba).

Caso práctico

Una de las partes de un estudio psicológico era pedir la fruta favorita de los participantes. El objetivo de esta pregunta es averiguar si hombres y mujeres tienen preferencias similares a la hora de elegir la fruta que desean comer. Para ello, se ha recogido información de 57 personas distintas que aceptaron participar en dicho estudio.

De todos los datos que se han extraído de la investigación, solo dos variables cualitativas se van a poner en una base de datos de Jamovi (formato .omv) denominada Fruta favorita: sexo (categorizado por hombre y mujer) y fruta (categorizado por plátano, kiwi, sandía, melón, melocotón, naranja, mandarina, piña, fresas, pera  y manzana). Ambas son variables cualitativas nominales, por lo que todo indica que se debe hacer una prueba Chi-cuadrado de independencia 2 · 11 (2 categorías de la primera variable · 11 de la segunda). Se puede acceder a los datos haciendo clic en el siguiente botón. El análisis se realizará en el software Jamovi (versión 2.3.28) en un ordenador Windows 10. No obstante, se recuerda que este mismo procedimiento se puede realizar en un ordenador Mac.

Procedimiento

Este tipo de prueba implica que debamos "personalizar" el contraste de hipótesis en función de la naturaleza de nuestras variables.

• Hipótesis nula [Ho]. Ambos sexos tienen preferencias similares a la hora de escoger una fruta.

• Hipótesis alternativa [H1]. Ambos sexos tienen preferencias distintas a la hora de escoger una fruta. 

En primer lugar, debemos acceder a la opción de Chi-cuadrado de independencia. Para ello, debemos estar en el menú de Análisis, hacer clic sobre el icono de Frecuencias y hacer clic sobre Muestras independientes: Prueba de asociación X². En la siguiente ventana de la izquierda deberemos trasladar nuestras dos variables objeto de estudio a las Filas y Columnas. La colocación de cada variable en filas o columnas de la tabla de contingencia no influye en absoluto en el análisis. Sin embargo, se recomienda colocar en las filas, la variable que más categorías o grupos tenga (Futa en este caso). 

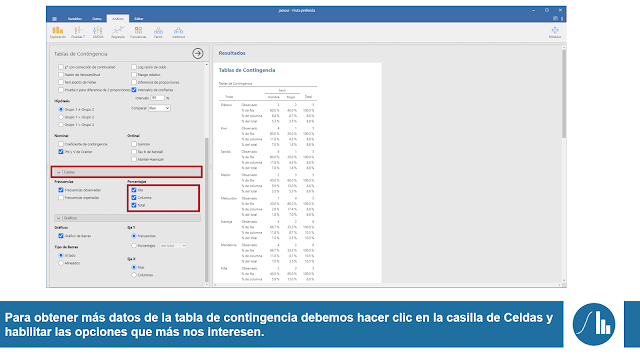
A continuación, debemos verificar el supuesto de que las frecuencias esperadas sean mayores que 5. Para ello, hacemos clic en la ventana de Celdas y hacemos clic sobre la ventana de Frecuencias esperadas. Si cada una de las frecuencias esperadas es mayor de 5, podemos continuar con nuestro análisis. 

Entonces, para solicitar la prueba Chi-cuadrado de independencia, hacemos clic en la casilla de Estadísticas. A continuación, nos aseguramos que la opción X² del apartado Pruebas esté marcada. Además, solicitaremos el tamaño del efecto de Phi y V de Cramer en el apartado de Nominal, tal y como se muestra en la siguiente imagen. Opcionalmente, se puede solicitar en el apartado de Gráficos el Gráfico de Barras. 

Resultados

En primer lugar debemos verificar la hipótesis que se confirma. Para ello, nos debemos fijar en el p-valor de la tabla X² y determinar con qué hipótesis nos quedamos. A continuación, si el p-valor es inferior a 0,050 se deberá estudiar el tamaño del efecto. Tal y como se puede ver en la siguiente imagen, la V de Cramer se interpreta como la fuerza de la relación entre ambas variables: cuanto más cerca esté de 0 la relación es mas débil y cuanto más cerca esté de 1 dicha relación será más sólida. Nótese que el coeficiente de Phi no se reporta puesto que se precisa que el número de categorías entre una y otra variable sea perfecto: por ejemplo, 3 . 3 o 5 · 5. 

En este ejemplo el p-valor es 0,658; lo que significa que se debe apoyar la hipótesis nula de que no hay diferencias significativas entre la variable sexo y la preferencia de frutas. Por tanto, no tiene sentido seguir analizando el tamaño del efecto V de Cramer (que aún así da un valor cercano a 0; que significa que la fuerza de la relación es muy débil).

Redacción e interpretación final

En este tipo de análisis es muy habitual reportar los resultados en forma de tabla de contingencia o tabla de doble entrada. Dentro de ella se suelen poner la frecuencias o los porcentajes para cada una de las categorías de la variable. Además, también se suele reportar el estadístico completo acompañado de los grados de libertad, el p-valor y el tamaño del efecto. 

Para redactar el párrafo de resultados se recomienda la siguiente estructura. En azul las partes que se deben adaptar a cada uno de los casos particulares:

• El test de independencia X² de Pearson (no) mostró una asociación significativa entre la variable nominal A y la variable nominal B (X² (grados de libertad) = estadístico; p-valor; tamaño del efecto). Se observa que es más probable que la categoría Z de la variable A (porcentaje) prefiera la categoría N de la variable B (porcentaje) que la categoría X de la variable A (porcentaje). 

• Pearson's X² of independence (did not) showe(d) a significant association between nominal variable A and nominal variable B (X² (degrees of freedom) = statistic; p-value; effect size). Category N of the variable A (percentage) was more likely to prefer category N of variable B (percentage) compared to category X of the variable A (percentage).

Jacob Sierra Díaz y Alti 

Jamovi | Introducción a la prueba de bondad de ajuste Chi-cuadrado

La prueba de bondad de ajuste Chi-cuadrado (X²; Chi-square Goodness-of-fit en inglés) sirve para verificar si la distribución observada de las variables independientes nominales (por ejemplo, color favorito) coincide con las distribución de frecuencias esperadas. En esencia, estamos hablando de un contraste de hipótesis:

• Hipótesis nula [Ho]. Las frecuencias observadas son coincidentes con las frecuencias esperadas. Esto quiere decir que las frecuencias de las categorías de la(s) variable(s) independiente(s) son como se esperaban.

• Hipótesis alternativa [H1]. Al menos una frecuencia observada no encaja con la frecuencia esperada. Esto quiere decir que las frecuencias de, por lo menos, una categoría de la variable independiente, no es como se esperaba.

Es recomendable que estas hipótesis se adapten a la naturaleza de nuestros datos específicos. Al no haber direccionalidad en este test, no podemos hablar de hipótesis de una cola o hipótesis de dos colas. Por tanto, tal y como se muestra en la siguiente imagen, lo único que necesitamos para hacer esta prueba es una variable nominal divida por categorías.

Caso práctico

Hoy hemos pedido a diez personas diferentes que sacasen una carta de una baraja de póker francés. Hemos apuntado simplemente los palos: corazones, diamantes, tréboles o picas. En la base de datos simplemente hemos puesto el identificador de cada persona (que corresponde al orden en el que ha sacado la carta con respecto al resto de personas) junto con el palo extraído. Los datos que se han extraído son los siguientes: el sujeto 1 ha extraído diamante, el 2 diamante, el 3 picas, el 4 corazones, el 5 trébol, el 6 corazones, el 7 picas, el 8 diamantes, el 9 picas, el 10 corazones, el 11 diamantes, el 12 tréboles, el 13 picas, el 14 corazones, el 15 tréboles, el 16 corazones, el 17 picas, el 18 diamantes, el 19 picas, el 20 corazones, el 21 tréboles, el 22 diamantes, el 23 picas, el 24 corazones, el 25 trébol, el 26 corazones, el 27 picas, el 28 tréboles, el 29 picas y el 30 corazones. Se desea conocer si los sujetos han elegido sus cartas de una manera aleatoria. 

Sabemos que un mazo de cartas de póker se suele componer de 52 cartas, de las cuales 13 son de cada palo. Al haber cuatro palos, un cuarto (1/4) es el 25% de extraer aleatoriamente cada palo de la mesa. Por tanto, esta información nos ayudará a configura la hipótesis de partida.

Estos datos ficticios se van a introducir en una base de datos de Jamovi (versión 2.3.287) para su posterior análisis. En concreto tendrá dos variables: ID y Palo. Todo este procedimiento se realizará en un ordenador con sistema operativo Windows 10. No obstante, este mismo procedimiento será idéntico en un ordenador Mac.

Procedimiento

Lo primero que tenemos que hacer, una vez conocido la naturaleza del experimento o investigación así como su finalidad, es configurar la hipótesis de investigación.

• Hipótesis nula [Ho]. Esta es la que deseamos que se cumpla en la mayoría de los casos (al contrario que otras pruebas de contraste de hipótesis). Los participantes extraen las cartas de manera aleatoria del mazo. Esto significa que debe haber un 25% de probabilidades de extraer cada uno de los palos. 

• Hipótesis alternativa [H1]. Los participantes no extraen las cartas de manera aleatoria. Esto significa que hay una probabilidad distinta al 25% de extraer cada uno de los palos.

Para poder realizar adecuadamente esta prueba se deber verificar simplemente un supuesto: que las frecuencias esperadas sean lo suficientemente grandes (esto es mayores que 5). Tal y como se muestra en la siguiente ilustración, este supuesto se verifica en la tabla de la Prueba de proporciones que se habilita en la opción de Frecuencias esperadas dentro de N Resultados (Chi-cuadrado de bondad de ajuste) en el menú Frecuencias, que está en el menú Análisis. Efectivamente, debemos verificar que las frecuencias esperadas sean mayores que 5 para poder dar por válido y continuar con esta prueba estadística.

Si hemos hecho el procedimiento anterior, de manera paralela hemos realizado el análisis de bondad de ajuste Chi-cuadrado. Recordemos que esto se habilita desde el menú Análisis, Frecuencias y N Resultados (Chi-cuadrado de bondad de ajuste). A continuación, introduciremos nuestra variable nominal objeto de estudio en su casilla correspondiente. Automáticamente se muestran los resultados en la parte derecha.

Resultados

Tenemos dos tablas como resultados. La que primero interesa ver es, curiosamente, la segunda. En concreto debemos ver si el p-valor es significativo o no para determinar la hipótesis que debemos apoyar. En este ejemplo, el p-valor de la prueba es 0,753 (muy superior a 0,050). Por tanto, debemos aceptar la hipótesis nula de que las frecuencias observadas coinciden con las frecuencias esperadas.

La primera tabla muestra las frecuencias observadas (de nuestra base de datos) y las frecuencias esperadas. Estas últimas frecuencias se calculan dividiendo la muestra entre las categorías de la variable (n/k). Por último, cabe destacar que esta prueba no contiene tamaños de efecto. 

Redacción e interpretación final

Este tipo de prueba requiere una explicación de las frecuencias junto con una justificación específica del valor que se le ha dado al contraste de hipótesis. Simplemente, recordar que el Chi-cuadrado se expresa con los grados de libertad entre paréntesis y el p-valor. A continuación se muestra el ejemplo de este caso práctico:

• De los 30 participantes del experimento, 6 han escogido una carta del palo diamantes, 9 del palo picas, 9 del palo de corazones y 6 del palo de tréboles. Se deseaba conocer si verdaderamente estas extracciones han sido puramente aleatorias. Por tanto, se ha efectuado la prueba de bondad de ajuste chi-cuadrado para verificar que la probabilidades de elección fuesen iguales o similares en los cuatro palos. Dicho contraste no muestran una significación estadística (X² (3) = 1,20; p = 0,753), sugiriendo la posibilidad de que los participantes seleccionaron sus cartas y palos de manera puramente aleatoria. Específicamente, se observa que tanto las picas como los corazones fueron extraído en un 30% cada uno; mientras que los diamantes y tréboles fueron extraídos en un 20% cada uno. 

Seguir aprendiendo

A continuación, aprenderemos a realizar una prueba Chi-cuadrado de independencia o Chi-cuadrado de Pearson que sirve para analizar la relación entre dos variables nominales. Haz cli en el siguiente botón para acceder al contenido.

Jacob Sierra Díaz y Alti

Jamovi | Introducción a la prueba F de Welch

De sobra sabemos que para realizar un ANOVA de un factor se deben tener en cuenta, entre otras cosas, dos supuestos: la normalidad de los datos y la homogeneidad de las variables. Cuando la normalidad de los datos no se satisface, se recomienda sustituir la prueba de ANOVA por la prueba de Kruskal-Wallis, que  es lo que se ha visto en la entrada anterior. 

Prueba F de Welch

¿Qué pasa cuando se satisface el supuesto de normalidad pero no el supuesto de homogeneidad? Pue que, básicamente, hay que realizar la prueba F de Welch, tal y como se muestra en la siguiente imagen. 

Procedimiento

La prueba F de Welch se aplica desde el menú Análisis, ANOVA y ANOVA de un factor (no desde el apartado inferior ANOVA).

Como se puede ver en la imagen superior, debemos seleccionar la Prueba de homogeneidad (y la de normalidad si no se ha verificado aún) en el apartado Comprobaciones de supuestos para verificar si es significativo el test de Levene. Entonces, si la p es inferior a 0,050 debemos asumir que no hay homogeneidad de varianzas entre los grupos y que, por tanto, se requieres solicitar la opción de No asumir iguales (Welch) en el apartado de Varianzas.

Resultados e interpretación

Los resultados de este análisis son muy similares que los resultados de un ANOVA. Simplemente se recomienda reportar la F junto con los grados de libertad 1 y los grados de libertad 2 (entre paréntesis) seguidos del p-valor. En esta ocasión no es posible extraer el tamaño del efecto.  Por supuesto, las pruebas post-hoc se interpretan de una manera similar a lo que hemos visto en la entrada del ANOVA. Haz clic en el siguiente botón para recordarlo.

Seguir aprendiendo

En la siguiente entrada descubriremos en qué consiste la prueba Chi-cuadrado de bondad de ajuste. Haz clic en el siguiente botón para acceder al contenido:

Jacob Sierra Díaz y Alti

Jamovi | Introducción a la prueba Kruskal-Wallis

Ya sabemos, siendo muy simplistas, que hay dos tipos de test estadísticos. Por un lado, tenemos los test paramétricos y por otro los test no paramétricos. Los supuestos de normalidad determinarán que tipo de test es el que tendremos que ejecutar. En las dos últimas entradas hemos visto la manera de realizar un ANOVA de un factor en Jamovi. Este tipo de test forma parte de la familia de test paramétricos. Puedes hacer clic en el siguiente botón para acceder a este contenido.

Pero, ¿qué pasa cuando queremos comparar tres o más grupos con respecto a una variable dependiente cuantitativa y no se puede satisfacer el supuesto de normalidad?. Pues que debemos recurrir a la prueba no paramétrica similar al ANOVA.

Prueba de Kruskal-Wallis

Al igual que ocurre con el ANOVA de un factor, la prueba Kruskal-Wallis está diseñada para contrastar la hipótesis nula (Ho) de que no hay diferencias en las medias entre tres (o más) grupos con respecto a una variable cuantitativa continua dependiente.

Tal y como se observa en la siguiente imagen, esta prueba se ejecuta cuando no se ha podido verificar la distribución normal de dicha variable cuantitativa continua dependiente.

Tal y como se introduce en la ilustración anterior, cuando no se puede asumir la distribución normal de los datos (de la variable dependiente) se debe efectuar la prueba Kruskal-Wallis.

Caso práctico

Un club de natación distribuye a sus nadadores en edad escolar en distintos niveles según una prueba de rendimiento que consiste en nadar 100 metros libres. Cuando un niño o niña quiere acceder al club se le realiza la prueba y, en función del tiempo que tarde en nadar 100 metros libres, se le clasifica en Medusa (nivel básico), Delfín (nivel intermedio), Tiburón (nivel avanzado) u Orca (nivel competitivo). El director del club sospecha que la prueba que se está realizando no está distribuyendo a los nadadores de manera adecuada. Por ello, ha recogido toda la información de los últimos dos años teniendo en cuenta el tiempo que duró cada nadador en hacer la prueba y la categoría en la que ha acabado. El objetivo es determinar si dentro de los grupos hay diferencias reales o si simplemente la clasificación se está haciendo de manera arbitraria y sesgada.

Los datos ficticios de esta investigación se han introducido en una base de datos de Jamovi (formato .omv) para su posterior análisis estadístico. Para este caso práctico se empleó la la versión 2.3.287 en un ordenador Windows 10. Se recuerda que el procedimiento que se va a mostrar a continuación es idéntico para ordenadores Mac. Puedes hacer clic en el siguiente botón para acceder a la base de datos cuyo nombre es Natación y practicar esta prueba.

Procedimiento

Como viene siendo habitual, en primer lugar debemos comprobar el supuesto de normalidad. Como es lógico, en este caso, el p-valor estará por encima de 0,050; estimando que la variable dependiente (segundos en este ejemplo) no sigue una distribución normal. Puedes hacer clic en el siguiente botón para recordar cómo se verifica este supuesto en Jamovi.

En este momento, ya sabemos que lo que tenemos que realizar es una prueba Kruskal-Wallis. Entonces, [1] accedemos al menú Análisis, y hacemos clic sobre el icono ANOVA. A continuación, hacemos clic sobre ANOVA de un factor Kruskal-Wallis en la sección No paramétrico. 

[2] Introduciremos la variable dependiente (en este caso 100_seg) en su espacio correspondiente y la variable de agrupación (en este caso Categoría) en su casilla correspondiente. 

[3] Hacemos clic sobre tamaño del efecto y sobre comparaciones dos a dos DSCF. Esta última es similar a las pruebas post-hoc que se hacen en el ANOVA.

* Por supuesto, como ocurre con el ANOVA, al no haber habido significatividad en el p-valor inicial de la prueba Kruskal-Wallis no hubiese tenido sentido realizar las comparaciones dos a dos DSCF. Aquí simplemente se expresan por cuestiones didácticas.

Resultados

Los resultados de la prueba Kruskal-Wallis se interpretan de una manera similar al ANOVA de un factor. En primer lugar, debemos tener en cuenta la pregunta del contraste de hipótesis: ¿existe alguna diferencia en la tendencia central de varias muestras? Por tanto, lo que hay que ver es si el p-valor de la prueba es estadísticamente significativo (p < 0,050). En caso afirmativo (no es este ejemplo) deberemos ver una especificación comparando los grupos. 

En este ejemplo, el director del club de natación tiene motivos para estar intranquilo puesto que o bien se está clasificando a los nadadores de manera arbitraria o bien la prueba de los 100 metros libres no es suficiente para determinar las diferencias por niveles. Esto es debido a que no hay diferencia significativas entre los cuatro grupos o niveles.

Sin ánimo de profundizar mucho en la forma de la prueba Kruskal-Wallis, cabe destacar que el método que realiza es una comprobación de los rangos medios de cada uno de los grupos (es decir, una diferencia de medianas); a diferencia de las pruebas paramétricas (ANOVA en este caso) que trabaja con medias.

Redacción e interpretación final

Los resultados se pueden redactar de manera similar que el ANOVA que vimos anteriormente. Una posible propuesta para reportar los resultados de esta prueba puede ser la siguiente: te. En azul se muestran las partes que se deben sustituir por los datos particulares de cada análisis:

• Tras usar la prueba Kruskal-Wallis, (no) hay una diferencia significativa en la variable dependiente objeto de estudio en comparación con los grupos o condiciones [Chi-cuadrado(grados de libertad) = Estadístico; p-valor; tamaño del efecto].

• Using a Kruskal-Wallis test, there is (no) a significant difference in the dependen variable under study across the groups or conditions [Chi-square(degrees of freedom) = Stastistic; p-value; effect size].

Seguir aprendiendo

El otro día aprendimos a hacer un ANOVA de un factor; hoy, en esta entrada, hemos aprendido a realizar la prueba Kruskal-Wallis para cuando no se satisface el supuesto de normalidad. A continuación, hay que aprender lo que hay que hacer cuando el supuesto de homogeneidad no se cumple. Haz clic en el siguiente botón para acceder a la prueba F de Welch.

Jacob Sierra Díaz y Alti

Jamovi | Análisis de la varianza (ANOVA)

En la entrada de ayer, aprendimos a realizar una ANOVA de un factor básico. En esa entrada vimos que si queremos obtener información más exhaustiva de algunos cálculos como el tamaño del efecto, no era recomendable realizar el ANOVA de un factor desde el apartado que vimos. Hoy, siguiendo con el ejemplo de ayer, vamos a profundizar en la opción que más relevante puede resultar para análisis mucho más profesionales. 

ANOVA de un factor

Ya se ha dicho en múltiples ocasiones que el ANOVA es el acrónimo de análisis de la varianza y que se usa cuando queremos comparar una variable independiente de tres o más grupos con una variable dependiente de tipo cuantitativa continua o discreta. También se dijo que para poder llevar a cabo este tipo de análisis se debían de cumplir dos supuestos:

•  Supuesto de normalidad de la variable dependiente (p-valor de la prueba Sapiro-Wilk > 0,050)

• Supuesto de homogeneidad de varianzas (p-valor del test de Levene > 0,050).

Puedes hacer clic en el siguiente botón para acceder a la entrada anterior y profundizar sobre este tema:

Caso práctico

Podríamos decir que esta entrada es una continuación o ampliación de la entrada de ayer. Por tanto, vamos a tomar el mismo caso práctico que ayer en el que comparábamos los resultados de un examen de trigonometría en tres grupos de 4º de la ESO en que se aplicaron distintas metodologías de enseñanza-aprendizaje.

Nuevamente, puedes pulsar en el siguiente botón para acceder a la entrada anterior, leer el caso práctico y acceder a la base de datos adjunta:

Procedimiento

Supongamos que la base de datos se ha cargado correctamente en el programa y que se han satisfecho los dos supuestos para realizar el ANOVA de un factor. 

[1] A diferencia del procedimiento que vimos ayer, vamos a hacer clic en el menú Análisis y en el icono ANOVA. A continuación, seleccionamos ANOVA (debajo de la opción ANOVA de un factor que vimos).

[2] Ahora, introduciremos la variable dependiente (en este caso Calificación) en su espacio correspondiente y la variable de agrupación (en este caso Grupo) en la casilla de factores fijos. Nótese de que en cada casilla nos aparecen unos iconos orientativos del tipo de variable que se deben introducir.

[3] A continuación, seleccionaremos del apartado Tamaño del Efecto la omega la cuadrado (w al cuadrado).

[4] Para volver a comprobar los supuestos de normalidad y homogeneidad, deberemos hacer clic sobre Comprobaciones de supuestos. Dentro de ahí, podremos hacer clic en Prueba de normalidad, Prueba de homogeneidad y Gráfica Q-Q.

[5] Hacemos clic en el siguiente botón (Pruebas Post-Hoc). Debemos llevar la variable dependiente (seguramente la única que haya) al lado derecho. A continuación, deberemos marcar la opción Tukey del apartado Corrección (ya vimos que este estadístico es para cuando tenemos homogeneidad de varianzas; aunque Bonferroni también puede funcionar bien en este caso) y la opción La d de Cohen del apartado Tamaño del efecto. 

Los procedimientos post-hoc se emplean cuando no hay indicios iniciales de diferencias grupales. Su funcionamiento es relativamente sencillo puesto que se basan en comparación por pares entre los grupos objeto de análisis (tal y como si fuera una prueba t para cada par de grupos). Como se puede apreciar en la imagen superior, en Jamovi tenemos cinco tipo de pruebas:

• Sin corrección: No hay corrección del Error Tipo I. Consiste en realizar distintas prueba t para cada para de grupos (lo que hace que se incremente la probabilidad de cometer errores Tipo I). No es recomendable esta opción.

• Tukey. Controla el Error Tipo I relativamente bien, aunque no es tan conservadora como Bonferroni. 

• Scheffe. Emplea una compleja fórmula para corregir y ajustar los posibles errores y sesgos.

• Bonferroni. Se trata de la prueba más conservadora. Es recomendable cuando hay pocos números de comparaciones. En esencia lo que hace es multiplicar el p-valor por el número de comparaciones post-hoc realizadas.

• Holm. Similar a Bonferroni, pero corrige el p-valor secuencialmente.

Como recomendación, se suele aplicar Tukey o Bonferroni.

[6] Por último, en el apartado Medias Marginales Estimadas debemos mover la variable dependiente a las medias marginales en Término 1, tal y como se muestra en la imagen. Además, seleccionaremos en el apartado de Resultados las opciones Gráfica de medias marginales y Tabla de medias marginales; y en el apartado Opciones generales, señalaremos Celdas con pesos iguales. 

Resultados

Como es habitual en Jamovi, los resultados aparecen de manera automática en el lado derecho. Lo principal es conocer la significación (p-valor) del ANOVA. Este deberá ser inferior a 0,050 para que se pueda considerar el análisis post-hoc. Recordemos que para el ANOVA, la hipótesis nula (Ho) es que no hay diferencia de medias entre los grupos; por el otro lado, la hipótesis alternativa (H1) afirma que hay diferencias significativas entre los grupos. 

• Ya vimos que lo que hay que reportar aquí es lo siguiente F (grados de libertad de la variable independiente, grados de libertad de los residuos) = Estadístico; p-valor; tamaño del efecto. En este ejemplo: F(2, 47) = 23,5; p-valor < 0,001; W² = 0,473.

Puesto que el p-valor es inferior a 0,050 podemos continuar viendo los resultados de las diferencias de medias y su significatividad. Aquí hay que ver que valor tiene mayor medias en la tabla correspondinete a las comparaciones post-hoc. Además, también puede ser relevante observar las medias marginales estimadas (columna de medias). En este ejemplo se observa que el grupo A (M = 4,17; DT = 1,42) obtuvo una calificación significativamente inferior (p = 0,013) al grupo B  (M = 5,12; DT = 1,56) y muy significativamente inferior (p < 0,001) al grupo C (M = 8; DT = 1,75).

Redacción e interpretación final

La redacción de este tipo de análisis estadístico es idéntico al visto en la entrada de ayer. Haz clic en el siguiente botón para acceder y recordar esta parte de redacción e interpretación final:

Seguir aprendiendo

En la siguiente entrada, veremos qué prueba realizar cuando el supuesto de normalidad no se ha podido satisfacer. Haz clic en el siguiente botón para acceder a la prueba Kruskal-Wallis. 

Jacob Sierra Díaz y Alti

Jamovi | Introducción al ANOVA de un factor

Una de las pruebas estadísticas más usadas y conocidas en Estadística es el análisis de la varianza, acortado como ANOVA (del inglés ANalysis Of VAriance). Como su propio nombre indica, se trata de una técnica que usa la comparación de varianzas entre las medias de diferentes muestras para poder realizar el contraste de hipótesis estadísticas. Sin ánimo de profundizar mucho en este momento sobre los fundamentos del ANOVA, diremos que hay tres tipos distintos de ANOVA. Hoy veremos cómo se realiza un análisis de la varianza de un factor, ANOVA de un factor o One-Way ANOVA (en inglés) con el programa Jamovi.

ANOVA de un factor

Anteriormente hemos visto que cuando tenemos una variable independiente cualitativa dicotómica (con dos grupos, como por ejemplo sexo) y una variable dependiente cuantitativa continua (como por ejemplo estatura en centímetros) podíamos comparar ambos grupos con el estadístico T de Student (análisis paramétrico), t de Welch (análisis paramétrico sin homogeneidad de varianzas) o U de Mann-Whitney (análisis no paramétrico).

¿Pero qué pasa si en lugar de tener una variable independiente dicotómica tenemos una variable con tres o más categorías? Pues en tal caso deberíamos de hacer un ANOVA de un factor. En efecto el ANOVA de un factor se emplea para descubrir diferencias estadísticamente significativas de una (o varias) variables dependientes cuantitativas cuando tenemos tres o más grupos, tal y como se muestra en la siguiente imagen.

Tal y como se introduce en la ilustración anterior, para realizar un ANOVA de un factor debemos tener en cuenta cuatro supuestos previos:

• La(s) variable(s) dependiente(s) objeto de estudio deben seguir una distribución normal.

• Las varianzas entre los dos grupos deben ser similares o idénticas; es decir, debe haber homogenización de varianzas.

• La variable dependiente objeto de estudio debe ser una variable cuantitativa continua.

• Las puntuaciones obtenidas para cada sujeto deben ser independientes entre grupos. 

Caso práctico

Un proyecto de investigación quiere analizar las mejores estrategias para la enseñanza de Matemáticas. Para ello, se ha encontrado un instituto de Educación Secundaria Obligatoria que, con el consentimiento de toda la comunidad educativa (incluyendo a las familias de los alumnos), permitirá llevar a cabo una parte de la investigación. 

Por tanto, para este caso, se pretende estudiar la mejor metodología para la enseñanza de la unidad didáctica de trigonometría. Se ha llevado a cabo tres metodologías distintas en tres clases distintas de 4º de la ESO (correspondiente con 15 y 16 años de edad): una se basará en la metodología tradicional de enseñanza con el libro de texto (libro), otra en la enseñanza basada en retos y desafíos (retos) y la última en la enseñanza asistida por ordenadores y tecnología (tecnología). Al finalizar la intervención, se realizará un examen de la materia. La clase de 4º A (que usó la metodología tradicional) tiene 18 estudiantes, al igual que la clase 4ºB (que usó la metodología de restos) y la clase 4ºC (que usó la metodología tecnológica) tiene 14 alumnos haciendo un total de 50 alumnos.

El objetivo es conocer qué metodología ha producido una mejora considerable en la calificación final (rendimiento académico). 

Los datos ficticios de esta investigación se han introducido en una base de datos de Jamovi (formato .omv) para su posterior análisis estadístico. Para este caso práctico se empleó la la versión 2.3.287 en un ordenador Windows 10. Se recuerda que el procedimiento que se va a mostrar a continuación es idéntico para ordenadores Mac. Puedes hacer clic en el siguiente botón para acceder a la base de datos cuyo nombre es Trigonometría y practicar el ANOVA de un factor. Se advierte que la base de datos contiene variables que no serán empleadas en este procedimiento.

Procedimiento

Vamos a comenzar por comprobar los cuatro supuestos más importantes que debemos cumplir para realizar este procedimiento (y que están descritos antes de la presentación de este caso práctico).

• Supuesto de normalidad. No se expondrá en esta entrada para no hacerla más larga. Puedes hacer clic en el siguiente botón para recordar y refrescar el procedimiento básico para comprobar este supuesto. 

• Dentro de la prueba ANOVA de un factor encontraremos una opción en el apartado Comprobaciones de supuestos denominada Prueba de Normalidad para comprobar dicho supuesto.

• Supuesto de homogeneidad de varianza. Se obtiene dentro de las opciones de la prueba ANOVA de un factor (que veremos a continuación), en el apartado Comprobaciones de supuestos. En este caso, se procede a examinar la homogeneidad con el test de Levene. Si el p-valor de dicho test es superior a 0,050 (no significativo) se puede asumir la homogeneidad de varianzas.

• Se confirma que la variable dependiente (calificaciones del examen) es una variable cuantitativa, en este caso discreta.

• Además, se confirma que las puntuaciones de dicha variable son independientes entre grupos. Cada alumno ha realizado su examen sin influencia de los resultados de otras clases. 

Ahora estamos listos para realizar el ANOVA de un factor. [1] Hacemos clic en el menú Análisis y hacemos clic sobre el icono ANOVA. A continuación, seleccionamos ANOVA de un factor.

[2] Introduciremos la variable dependiente (en este caso Calificación) en su espacio correspondiente y la variable de agrupación (en este caso Grupo) en su casilla correspondiente. 

[3] Si no lo hemos hecho antes, en el apartado de Comprobaciones de Supuestos, seleccionamos la opción Prueba de homogeneidad. [4] En función del resultado de la p-valor del test de Levene debermos marcar en el apartado de Varianzas el test de Welch [cuando p < 0,050] o el test de Fisher [cuando p > 0,050].

[5] Adicionalmente, podremos solicitar la Tabla de descriptivas en el apartado de Estadísticas adicionales.

[6] Cabe mencionar que un ANOVA es un estadístico ómnibus que bajo el contraste de hipótesis nula verifica que las medias de los tres o más grupos es la misma. Esto significa que no sabemos la orientación de la diferencia (es decir, si el grupo A es mayor que el grupo B; por ejemplo). Y es por ello que es necesario realizar las denominadas pruebas Post-Hoc. No obstante, para realizar pruebas Post-Hoc se deberá haber obtenido una significación en el p-valor del ANOVA. Entonces, para invocar pruebas Post-Hoc, podremos hacer clic en los apartados correspondientes y clicar sobre Tukey si las varianzas se han demostrado iguales. Por el contrario, si las varianzas son distintas se deberá usar Games-Howell. Además, en el apartado de Estadísticas, se recomienda seleccionar Diferencia de medias, significación, resultados de la prueba y marcaje de comparaciones significativas.

Diferencia entre ANOVA de un factor y ANOVA

Habrás podido apreciar que cuando vamos a usar un ANOVA en el menú general de Análisis aparecen dos tipos distintos de ANOVA (véase la ilustración de la derecha): ANOVA de un factor (el que hemos hecho) y ANOVA. ¿Qué diferencia hay? Que el ANOVA incluye muchas más opciones e información, los resultados serán los mismos por uno u otro método pero con el segundo se podrán mostrar más resultados. Para un análisis de datos más complejo, se recomienda siempre hacerlo desde la opción ANOVA y no desde la que hemos visto aquí.

Resultados

Como ya se ha visto en la ilustración grande anterior, lo primero que tenemos que hacer es verificar si nuestros resultados son estadísticamente significativos, es decir, si la p-valor es inferior a 0,050. El ANOVA de un factor es un contraste de hipótesis en el que se comprueba que todas las muestras proceden de la misma población (hipótesis nula), tal y como se refleja en la siguiente ilustración. 

- En este caso, el ANOVA de nuestros resultados es estadísticamente significativo (p < 0,050). 

- Para reportar este estadístico debemos escribir el valor de la F junto con los grados de libertad: uno de ellos es el de la variable independiente (Grupo en este ejemplo) que es el número de categorías menos uno (K - 1; 3 - 1 = 2) y el otro son los residuos o la varianza intra-sujeto que se calcula por el número de muestra menos el número de grupos (n - K; 50 - 3 = 47). ¡Nota importante! El primer tipo de grado de libertad aparece como gl1 (2 en este caso) y el segundo como gl2 (47 en este caso). Esta información se desglosa de otra manera en la opción de ANOVA.

- Por último, tenemos que reportar el tamaño del efecto que, en este caso, es preferible el omega al cuadrado. ¡Ojo! En la opción de ANOVA de un factor no aparece este tamaño, siendo preciso ejecutar la opción de ANOVA anteriormente citada. 

Volviendo a nuestro ejemplo, se observa que hay diferencias estadísticamente significativas en los tres grupos. Haciendo un análisis más específico con las pruebas Post-Hoc se puede apreciar que el grupo que disfrutó de una metodología tecnológica obtuvo mejores calificaciones que el grupo con la metodología de retos (grupo B) y con la metodología tradicional (grupo A).

Redacción e interpretación final

Lo que debemos reportar en los informes o en el artículo científico es el estadístico F junto con los dos grados de libertad, el p-valor y el tamaño del efecto (índice que no se ha extraído aquí). A continuación, en el caso de que el p-valor sea significativo, se deberá realizar un análisis de las pruebas post-hoc destacando las diferencias de medias, el estadístico t y la significatividad.

Una propuesta de redacción del ANOVA de un factor tanto en español como en inglés puede ser la siguiente. En azul se muestran las partes que se deben sustituir por los datos particulares de cada análisis:

• (No) Hay diferencias significativas en la variable dependiente objeto de estudio entre los grupos o condiciones [F(grados de libertad 1; grados de libertad 2) = Estadístico; p-valor; tamaño del efecto].

• There is (no) significant differences in the dependen variable under study across the groups or conditions [F(degrees of freedom 1, degrees of freedom 2) = Stastistic; p-value; effect size].

Seguir aprendiendo

A continuación, en la siguiente entrada, veremos la opción de ANOVA que hemos introducido en esta entrada. Haz clic en el siguiente botón para profundizar en el análisis factorial con Jamovi:

Jacob Sierra Díaz y Alti

Jamovi | Introducción a la prueba t de Welch

Anteriormente hemos visto el procedimiento tanto paramétrico (T de Student) como no paramétrico (U de Mann-Whitney) para analizar las diferencias significativas entre dos grupos con respecto a una o varias variables dependientes. Sin embargo, existe una tercera prueba que es interesante conocer: la t de Welch. 

Prueba t de Welch

En términos coloquiales, la t de Welch (Welch's t-test en inglés) es la "hermana" de la prueba T de Student, es decir, son estadísticos que forman parte del grupo de procedimientos paramétricos (que los datos muestrales de las variables dependientes proceden de poblaciones que siguen una distribución normal). Diferenciaremos a ambas en función de la letra mayúscula o minúscula. 

La diferencia más importante entre la t de Welch y la T de Student es que la primera puede "funcionar" sin necesidad de asumir la igualdad de varianzas. La siguiente ilustración muestra los supuestos que se deben cumplir para la familia de estadísticos de las pruebas t para muestras independientes (independent t-test en inglés):

En efecto, la única diferencia que existe entre la T de Student y la t de Welch es el supuesto de homogeneidad de varianzas, que se puede examinar mediante el test de Levene. Ahora bien, antes de estudiar la homogeneidad de varianzas se deberá determinar la idoneidad entre la estadística paramétrica o la no paramétrica. Para ello, primeramente, deberemos analizar la distribución de la variable dependiente, con el objetivo de ver si esta sigue una distribución normal. Haz clic en el siguiente botón para recordar el análisis de los supuestos que normalidad que no se reiterarán en esta entrada para no hacerla más densa:

En definitiva, usaremos la t de Welch cuando queramos comprobar las diferencias entre dos grupos independientes con respecto a una variable dependiente cuantitativa continua siempre y cuando siga una distribución normal pero no se pueda garantizar la homogeneidad de varianzas.

Caso práctico

Una humilde investigación pretende analizar la cantidad de libros que se han leído en el último año teniendo en cuenta la mayoría de edad. Para ello, se ha preguntado al azar a 8 personas (4 menores de edad y 4 mayores de edad) por los libros que leyeron durante el año pasado. Con ello, se pretende averiguar si hay una diferencia estadísticamente significativa entre la cantidad de libros leídos por las personas mayores de edad con respecto a las personas menores de edad.

Estos datos ficticios se introdujeron en una base de datos de Jamovi (formato .omv) para su posterior análisis estadístico. Para este ejemplo se empleó la la versión 2.3.287 en un ordenador Windows 10. Se recuerda que el procedimiento que se va a mostrar a continuación en un ordenador Mac es idéntico. Puedes hacer clic en el siguiente botón para acceder a la base de datos cuyo nombre es Lectura y practicar la ejecución de la prueba t de Welch.

Procedimiento

Se debe recordar que para proceder con esta prueba, previamente se debe haber analizado la distribución normal de la variable dependiente objeto de estudio (en este caso libros leídos en un año). Puedes hacer clic en el botón verde anterior para recordar cómo se realiza este procedimiento con Jamovi. Nótese que esta misma prueba se puede hacer a continuación en el apartado de Comprobaciones de Supuestos. 

Ahora, en el menú Análisis pulsamos sobre Pruebas T y, a continuación, sobre Prueba T para muestras independientes. A continuación, introduciremos la variable dependiente (en este caso Libros) en su espacio correspondiente y la variable de agrupación de dos categorías (en este caso Mayor_Edad; con los valores Sí y No) en su casilla correspondiente. Anteriormente, como ya habíamos analizado el supuesto de normalidad, sabíamos qué prueba seleccionar. En este caso, y en otros similares en los que no tenemos ni idea de la naturaleza de la distribución, se recomienda realizar las pruebas de homogeneidad y de normalidad antes de seleccionar la prueba estadística adecuada en el apartado correspondiente. 

Ya sabemos que los datos de la variable dependiente se distribuyen normalmente (puesto que se ha realizado previamente la prueba de Shapiro-Wilk --no expuesta en esta entrada--). Ahora, debemos confirmar que la homogeneidad de varianza sea similar para determinar si se realiza la prueba T de Student o la prueba t de Welch. Para ello, tendremos que invocar el test de Levene seleccionando, en el apartado de Comprobaciones de supuestos,  la Prueba de Homogeneidad.

• En resumidas cuentas, para que se cumpla el supuesto de homogeneidad de variables con el test de Levene la significación debe ser mayor que 0,050 (p-valor > 0,050).

Cuando ya sepamos esta información, siguiendo con la ilustración anterior, deberemos seleccionar la prueba correspondiente en el apartado de Prueba (en este caso, según los supuestos, la prueba t de Welch). Además, será interesante seleccionar la diferencia de medias, el tamaño del efecto y las estadísticas descriptivas del apartado Estadísticas Adicionales que se mostrarán en la ventana de resultados; tal y como se muestra en la siguiente imagen:

Resultados

La interpretación de la prueba t de Welch es muy similar a la de la prueba T de Student y U de Mann-Whitney. Simplemente, debemos mirar el p-valor para determinar si hay diferencias estadísticamente significativas (p-valor < 0,050) en las medias de los dos grupos, tal y como se muestra en la siguiente imagen:

En este ejemplo, se observa que el p-valor es mayor a 0,050. Por tanto, tenemos evidencias suficientes para respaldar hipótesis nula y asegurar que las medias de los grupos son similares. Por tanto, no hay diferencias estadísticamente significativas entre los libros leídos por personas mayores de edad (M = 2; DT = 0) y los libros leídos por menores de edad (M = 3; DT = 1,15) [t(3) = -1,73; p = 0,182; d = -1.22]. No obstante, nuevas evidencias son necesarias para confirmar esta tendencia puesto que el tamaño muestral (n = 8) es extremadamente bajo. 

Redacción e interpretación final

La redacción de los resultados es similar a las pruebas de esta misma familia vistas anteriormente. Sencillamente tendremos que reportar el estadístico t junto con los grados de libertad, seguido del p-valor y del valor del tamaño del efecto.

A continuación se muestra una propuesta de redacción tanto en español como en inglés. En azul todos aquellos elementos que se deben sustituir en función de los resultados particulares.

• Mediante la prueba estadística t de Welch, (no) se aprecia una diferencia estadísticamente significativa en la variable dependiente objeto de estudio entre el grupo A (Media; Desviación Típica) y el grupo B (Media; Desviación Típica) [t(grados de libertad) = Estadístico; p-valor; tamaño del efecto d].

• Using a Welch's t-test, there was (not) a statistically significant difference in the dependent variable between group A (Mean; Standard Deviation) and group B (Mean; Standard Deviation) [t(degrees of freedom) = Statistic; p-value; d-effect size].

Seguir aprendiendo

Lo siguiente que vamos a ver es un análisis similar a los tres que hemos visto en estas últimas entradas pero teniendo en cuenta que la variable independiente puede tener tres o más grupos. Haz clic en el siguiente botón para acceder al procedimiento para calcular un ANOVA de un factor:

Jacob Sierra Díaz y Alti