SPSS Básico | Prueba T de Student (muestras independientes)

El estadístico T para muestras independientes es una prueba estadística de contraste de hipótesis que se usa cuando se desea comparar las medias de (únicamente) dos grupos de participantes diferentes. El término "muestras independientes" alude al hecho de que las medias proceden de dos poblaciones independientes. Esto quiere decir que los participantes de un grupo son distintos a los participantes de otro grupo en una o varias variables independientes. Un ejemplo muy característico de este caso sería la variable independiente sexo; cuyos valores son (únicamente) masculino o femenino. 

La configuración ideal para esta prueba es que los sujetos que forman cada uno de los dos grupos de un hipotético experimento se hayan asignado aleatoriamente a dichos grupos con el fin de que cualquier diferencia se deba al experimento y no a otros factores externos. 

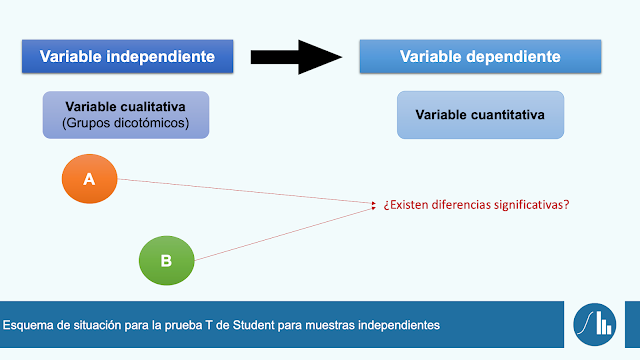
En resumidas cuentas, tal y como se muestra en el siguiente esquema, cuando se asumen los supuestos de normalidad y se tiene que comparar una (o varias) variables dependientes cuantitativas en únicamente dos grupos, emplearemos la prueba T de Student para muestras independientes.

Caso práctico

El objetivo principal de una investigación es averiguar si un programa de entrenamiento aeróbico
intensivo de una semana mejora significativamente la cantidad de oxígeno que el organismo puede absorber, transportar y consumir en un momento determinado (VO2 máximo). 

Para ello, se dispone de una muestra de 100 participantes que se distribuirán aleatoriamente en dos grupos de 50 participantes cada uno: 

• El primer grupo recibirá el paquete de entrenamiento aeróbico intensivo (grupo experimental)

• El segundo grupo recibirá sesiones prácticas tradicionales (grupo de control). 

Tras la semana de intervención (aplicación de ambos programas de entrenamiento), se midió y se registró el VO2 máximo de cada participante en una prueba aeróbica con el tapiz rodante. 

Estos datos ficticios se introdujeron en una base de datos de SPSS (formato .sav) para su posterior análisis estadístico. Se empleó la versión 27 de IBM-SPSS en Windows 10. Puedes hacer clic en el siguiente botón para acceder a la base de datos y practicar la ejecución de la prueba que se describe a continuación. La contraseña de dicha base de datos es Stadistica. 

Procedimiento

Una vez abierta la base de datos en SPSS deberemos realizar un estudio de la normalidad de los datos. Esto no se va a cubrir en esta entrada, pero sí que cabe recordar que para poder efectuar la prueba T-Student para muestras independientes, la significación (p-valor) del contraste de hipótesis de la prueba de normalidad que se realice deberá ser superior a 0,050.

Para hacer el análisis de la prueba T-Student usaremos la interfaz gráfica de usuario de SPSS. En primer lugar, daremos clic a Analizar, buscaremos Comparar media y haremos clic en Prueba T de muestras independientes...

En la siguiente ventana, deberemos introducir las variable dicotómica (variable que tiene dos agrupaciones correspondientes con el grupo experimental o grupo de control) en Variable de agrupación. Ahora, meteremos la(s) variable(s) dependiente(s) en Variable de prueba. Recuerda que para meter las variables deberemos seleccionar la variable y hacer clic en la flecha correspondiente al lado del tipo de variable que se quiera introducir. 

En este caso particular, meteremos la variable Grupo en Variable de agrupación y la variable VO2max en variable de prueba, tal y como se muestra en la siguiente imagen.

Ahora, tenemos que definir los grupos de la variable dicotómica. Para ello, nos tendremos que acordar de la codificación que hemos usado. Hacemos clic en Definir grupos... e introducimos el código numérico que tengamos para el grupo 1 (normalmente 1 o 0) y el código numérico usado para el grupo 2 (normalmente 1 o 2). Recuerda que no importa el orden en el que se pongan los grupos.

En este caso, hemos codificado el grupo experimental como 1 y el grupo control como 2. Entonces, introduciremos en el Grupo 1 el 1 y en el Grupo 2 el 2, tal y como se muestra en la siguiente imagen.

Finalmente, haremos clic en Aceptar. 

Resultados

Varias son las tablas que generará SPSS (versión 27) para la prueba T de Student de muestras independientes. 

La primera tabla tiene el nombre de Estadísticas de grupo. En ella se refleja la muestra (n) , la media, la desviación estándar y la media del error estándar de cada grupo. En versiones de SPSS anteriores, a la media del error estándar se le conocía como error típico de la media. Se trata de un valor que cuantifica las desviaciones de la media muestran teniendo en cuenta la media poblacional. Dicho en otras palabras,  se trata de un valor que indica cuánto se apartan los valores de la media de la población. Este valor sirve para elaborar los intervalos de confianza de la media correspondiente.

La siguiente tabla es la que más nos interesa. Tiene el nombre de Prueba de muestras independientes. puesto que recoge los resultados de la prueba propiamente dicha. Aquí, en primer lugar, debemos observar las columnas correspondientes a la prueba de Levene de igualdad de varianzas. Este test verifica la homocedsticidad (uno de los requisitos para asumir la distribución normal de los datos). En concreto, debemos observar el p-valor (sig.) para tomar una decisión:

• p-valor (sig.) superior a 0,050 | Es lo deseable. Significa que podemos suponer igualdad de varianzas. Entonces, continuaremos interpretando esta tabla atendiendo exclusivamente a la primera fila de resultados.

• p-valor (sig.) inferior a 0,050 | En este caso debemos suponer que las varianzas de ambos grupos son distintas. 

En efecto, la interpretación del test de Levene es contraria a lo que en el resto de pruebas debemos mirar del p-valor. En este caso, lo deseable es encontrar el p-valor superior a 0,050.

A continuación, de manera práctica, deberíamos mirar el p-valor (sig.) de la siguiente parte de esta tabla. En este ejemplo se mirará la primera fila puesto que con el test de Levene se asume igualdad de varianzas (p-valor superior a 0,050). Aquí pueden ocurrir dos cosas:

• p-valor (sig.) superior a 0,050 | Las medias son iguales en ambos grupos. En este caso se acepta la hipótesis nula de que los resultados de la variable dependiente son independientes a cada grupo; es decir, las posibles diferencias entre grupos se debe al azar y no hay pruebas de que procedan de la intervención.

• p-valor (sig.) inferior a 0,050 | Lo ideal (en la mayoría de casos). Las medias son distintas en cada grupo. En esta situación, la variable dependiente depende o está relacionada con la variable independiente. Esto significa que los resultados de la variable dependiente (VO2 max en este ejemplo) están condicionados al grupo de la variable independiente (grupo experimental y grupo control en este ejemplo). En otras palabras, no hay pruebas para rechazar que los resultados se deban al azar y es (estadísticamente) probable que las diferencias entre grupos se deban, precisamente a la distribución de los grupos (y sus intervenciones experimentales distintas).

Esto es lo que habría que mirar de manera práctica. Ahora bien, tenemos que reportar otra información contenida en esta tabla. En concreto, habría que reportar el estadístico t acompañado de su nivel de significación (p-valor). También sería interesante reportar los límites del intervalo de confianza. En concreto, debemos observar el límite inferior y superior del intervalo de confianza: si dentro de ese rango no se incluye el 0, se puede asumir con total seguridad que se puede rechazar la hipótesis nula (Ho) de igualdad de medias en ambos grupos.

Para saber cuánta ha sido la diferencia de medias, deberemos ir a la tabla anterior (Prueba de muestras independientes).

Por último, las versiones recientes de SPSS (como es el caso de la versión 27), ofrecen una tercera tabla. Esta tabla tiene el título de Tamaños de efecto de muestras independientes. En concreto, podemos observar tres estadísticos del tamaño del efecto que siempre son recomendables acompañar con el p-valor. El más usado en este tipo de pruebas es la d de Cohen. Este test es muy apropiado para la comparación de medias y nos da información sobre la diferencia media estandarizada de un efecto. Su interpretación es muy sencilla: el tamaño del efecto es grande (y por tanto deseable) cuando su valor es superior a 0,800.

Interpretación

Inferencia estadística | Para realizar una interpretación correcta de esta prueba debemos recordar que se trata de un test de contraste de hipótesis en la que la hipótesis nula es que no hay diferencias de medias en las dos muestras (o grupos) independientes y, que en caso de existir, se debe exclusivamente al azar.

La interpretación de estos resultados es muy sencilla de realizar. Simplemente deberemos informar si hay diferencias significativas (H1) o no (Ho). Para ello, necesitaremos apuntar los valores que se han dicho anteriormente de las tablas de SPSS de la siguiente forma: t (grados de libertad - gl) = estadístico t; p = valor de sig.. Previamente se deberán reportar las medias y las desviaciones típicas de ambos grupos. Aunque no es necesario, se puede reportar los resultados e interpretación de la prueba de Levene. Lo que sí que es recomendable es reportar el tamaño del efecto d de Cohen (junto con su interpretación). Se recomienda usar un tiempo verbal pasado. 

Veamos un ejemplo básico en español y en inglés sobre cómo poder reflejar los resultados de nuestro caso práctico:

• Se observaron diferencias significativas en el VO2 máximo entre el grupo experimental (M = 65,04; DT = 1,77) y el grupo control (M = 60,04; DT = 1,98) [t (98) = -13,270; p < 0,001]. El tamaño del efecto se considera grande (d = 1,884).

• There was a significant difference in VO2 max between the experimental group (M = 65.04; SD = 1.77) and the control group (M = 60.04; SD = 1.98) [t (98) = -13.70; p <0.001]. Effect size was assumed as large (d = 1.884).

Jacob Sierra Díaz y Alti